Hot Contents: The Regular Form

Sliding mode control

In control theory, sliding mode control, or SMC, is a nonlinear control method that alters the dynamics of a nonlinear system by application of a discontinuous control signal that forces the system to "slide" along a cross-section of the system's normal behavior. The state-feedback control law is not a continuous function of time. Instead, it can switch from one continuous structure to another based on the current position in the state space. Hence, sliding mode control is a variable structure control method. The multiple control structures are designed so that trajectories always move toward an adjacent region with a different control structure, and so the ultimate trajectory will not exist entirely within one control structure. Instead, it will slide along the boundaries of the control structures. The motion of the system as it slides along these boundaries is called a sliding mode and the geometrical locus consisting of the boundaries is called the sliding (hyper)surface. In the context of modern control theory, any variable structure system, like a system under SMC, may be viewed as a special case of a hybrid dynamical system as the system both flows through a continuous state space but also moves through different discrete control modes.

Control scheme

Consider a nonlinear dynamical system described by

$\dot{\mathbf{x}}(t)=f(\mathbf{x},t) + B(\mathbf{x},t)\,\mathbf{u}(t)$

$(1)\,$

where

$\mathbf{x}(t) \triangleq \begin{bmatrix}x_1(t)\\x_2(t)\\\vdots\\x_{n-1}(t)\\x_n(t)\end{bmatrix} \in \mathbb{R}^n$

is an $n$ -dimensional state vector and

$\mathbf{u}(t) \triangleq \begin{bmatrix}u_1(t)\\u_2(t)\\\vdots\\u_{m-1}(t)\\u_m(t)\end{bmatrix} \in \mathbb{R}^m$

is an $m$ -dimensional input vector that will be used for state feedback. The functions $f: \mathbb{R}^n \times \mathbb{R} \mapsto \mathbb{R}^n$ and $B: \mathbb{R}^n \times \mathbb{R} \mapsto \mathbb{R}^{n \times m}$ are assumed to be continuous and sufficiently smooth so that the Picard–Lindelöf theorem can be used to guarantee that solution $\mathbf{x}(t)$ to Equation (1) exists and is unique.

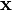A common task is to design a state-feedback control law $\mathbf{u}(\mathbf{x}(t))$ (i.e., a mapping from current state $\mathbf{x}(t)$ at time $t$ to the input $\mathbf{u}$ ) to stabilize the dynamical system in Equation (1) around the origin $\mathbf{x} = [0, 0, \ldots, 0]^{\text{T}}$ . That is, under the control law, whenever the system is started away from the origin, it will return to it. For example, the component $x1$ of the state vector $\mathbf{x}$ may represent the difference some output is away from a known signal (e.g., a desirable sinusoidal signal); if the control $\mathbf{u}$ can ensure that $x1$ quickly returns to $x1 = 0$ , then the output will track the desired sinusoid. In sliding-mode control, the designer knows that the system behaves desirably (e.g., it has a stable equilibrium) provided that it is constrained to a subspace of its configuration space. Sliding mode control forces the system trajectories into this subspace and then holds them there so that they slide along it. This reduced-order subspace is referred to as a sliding (hyper)surface, and when closed-loop feedback forces trajectories to slide along it, it is referred to as a sliding mode of the closed-loop system. Trajectories along this subspace can be likened to trajectories along eigenvectors (i.e., modes) of LTI systems; however, the sliding mode is enforced by creasing the vector field with high-gain feedback. Like a marble rolling along a crack, trajectories are confined to the sliding mode.

The sliding-mode control scheme involves

Selection of a hypersurface or a manifold (i.e., the sliding surface) such that the system trajectory exhibits desirable behavior when confined to this manifold.
Finding feedback gains so that the system trajectory intersects and stays on the manifold.

Because sliding mode control laws are not continuous, it has the ability to drive trajectories to the sliding mode in finite time (i.e., stability of the sliding surface is better than asymptotic). However, once the trajectories reach the sliding surface, the system takes on the character of the sliding mode (e.g., the origin $\mathbf{x}=\mathbf{0}$ may only have asymptotic stability on this surface).

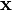The sliding-mode designer picks a switching function $\sigma: \mathbb{R}^n \mapsto \mathbb{R}^m$ that represents a kind of "distance" that the states $\mathbf{x}$ are away from a sliding surface.

Existence of closed-loop solutions

Note that because the control law is not continuous, it is certainly not locally Lipschitz continuous, and so existence and uniqueness of solutions to the closed-loop system is not guaranteed by the Picard–Lindelöf theorem. Thus the solutions are to be understood in the Filippov sense. Roughly speaking, the resulting closed-loop system moving along $\sigma(\mathbf{x}) = \mathbf{0}$ is approximated by the smooth dynamics $\dot{\sigma}(\mathbf{x}) = \mathbf{0}$ ; however, this smooth behavior may not be truly realizable. Similarly, high-speed pulse-width modulation or delta-sigma modulation produces outputs that only assume two states, but the effective output swings through a continuous range of motion. These complications can be avoided by using a different nonlinear control design method that produces a continuous controller. In some cases, sliding-mode control designs can be approximated by other continuous control designs.

Theoretical foundation

The following theorems form the foundation of variable structure control.

Theorem 1: Existence of Sliding Mode

Consider a Lyapunov function candidate

$V(\sigma(\mathbf{x}))=\frac{1}{2}\sigma^{\text{T}}(\mathbf{x})\sigma(\mathbf{x})=\frac{1}{2}\|\sigma(\mathbf{x})\|_2^2$

$(3)\,$

where $\|\mathord{\cdot}\|$ is the Euclidean norm (i.e., $\|\sigma(\mathbf{x})\|_2$ is the distance away from the sliding manifold where $\sigma(\mathbf{x})=\mathbf{0}$ ). For the system given by Equation (1) and the sliding surface given by Equation (2), a sufficient condition for the existence of a sliding mode is that

$\underbrace{ \overbrace{\sigma^{\text{T}}}^{\tfrac{\partial V}{\partial \sigma}} \overbrace{\dot{\sigma}}^{\tfrac{\operatorname{d} \sigma}{\operatorname{d} t}} }_{\tfrac{\operatorname{d}V}{\operatorname{d}t}} < 0 \qquad \text{(i.e., } \tfrac{\operatorname{d}V}{\operatorname{d}t} < 0 \text{)}$

in a neighborhood of the surface given by $\sigma(\mathbf{x})=0$ .

Roughly speaking (i.e., for the scalar control case when $m = 1$ ), to achieve $\sigma^{\text{T}} \dot{\sigma} < 0$ , the feedback control law $u(\mathbf{x})$ is picked so that $σ$ and $\dot{\sigma}$ have opposite signs. That is,

Reachability: Attaining sliding manifold in finite time

To ensure that the sliding mode $\sigma(\mathbf{x})=\mathbf{0}$ is attained in finite time, $\operatorname{d}V/{\operatorname{d}t}$ must be more strongly bounded away from zero. That is, if it vanishes too quickly, the attraction to the sliding mode will only be asymptotic. To ensure that the sliding mode is entered in finite time,

$\frac{\operatorname{d}V}{\operatorname{d}t} \leq -\mu (\sqrt{V})^{\alpha}$

where $μ > 0$ and $0 < \alpha \leq 1$ are constants.

Explanation by comparison lemma

This condition ensures that for the neighborhood of the sliding mode $V \in [0,1]$ ,

$\frac{\operatorname{d}V}{\operatorname{d}t} \leq -\mu (\sqrt{V})^{\alpha} \leq -\mu \sqrt{V}.$

So, for $V \in (0,1]$ ,

$\frac{ 1 }{ \sqrt{V} } \frac{\operatorname{d}V}{\operatorname{d}t} \leq -\mu,$

which, by the chain rule (i.e., $\operatorname{d}W/{\operatorname{d}t}$ with $W \triangleq 2 \sqrt{V}$ ), means

$\mathord{\underbrace{D^+ \Bigl( \mathord{\underbrace{2 \mathord{\overbrace{\sqrt{V}}^{ {} \propto \|\sigma\|_2}}}_{W}} \Bigr)}_{D^+ W \, \triangleq \, \mathord{\text{Upper right-hand } \dot{W}}}} = \frac{ 1 }{ \sqrt{V} } \frac{\operatorname{d}V}{\operatorname{d}t} \leq -\mu$

where $D$ is the upper right-hand derivative of $2 \sqrt{V}$ and the symbol $\propto$ denotes proportionality. So, by comparison to the curve $z(t) = z0 - μt$ which is represented by differential equation $\dot{z} = -\mu$ with initial condition $z(0) = z0$ , it must be the case that $2 \sqrt{V(t)} \leq V_0 - \mu t$ for all $t$ . Moreover, because $\sqrt{V} \geq 0$ , $\sqrt{V}$ must reach $\sqrt{V}=0$ in finite time, which means that $V$ must reach $V = 0$ (i.e., the system enters the sliding mode) in finite time. Because $\sqrt{V}$ is proportional to the Euclidean norm $\|\mathord{\cdot}\|_2$ of the switching function $σ$ , this result implies that the rate of approach to the sliding mode must be firmly bounded away from zero.

Consequences for sliding mode control

In the context of sliding mode control, this condition means that

$\underbrace{ \overbrace{\sigma^{\text{T}}}^{\tfrac{\partial V}{\partial \sigma}} \overbrace{\dot{\sigma}}^{\tfrac{\operatorname{d} \sigma}{\operatorname{d} t}} }_{\tfrac{\operatorname{d}V}{\operatorname{d}t}} \leq -\mu ( \mathord{\overbrace{\| \sigma \|_2}^{\sqrt{V}}} )^{\alpha}$

where $\|\mathord{\cdot}\|$ is the Euclidean norm. For the case when switching function $σ$ is scalar valued, the sufficient condition becomes

$\sigma \dot{\sigma} \leq -\mu |\sigma|^{\alpha}$ .

Taking $α = 1$ , the scalar sufficient condition becomes

$\operatorname{sgn}(\sigma) \dot{\sigma} \leq -\mu$

which is equivalent to the condition that

$\operatorname{sgn}(\sigma) \neq \operatorname{sgn}(\dot{\sigma}) \qquad \text{and} \qquad |\dot{\sigma}| \geq \mu > 0$ .

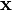That is, the system should always be moving toward the switching surface $σ = 0$ , and its speed $|\dot{\sigma}|$ toward the switching surface should have a non-zero lower bound. So, even though $σ$ may become vanishingly small as $\mathbf{x}$ approaches the $\sigma(\mathbf{x})=\mathbf{0}$ surface, $\dot{\sigma}$ must always be bounded firmly away from zero. To ensure this condition, sliding mode controllers are discontinuous across the $σ = 0$ manifold; they switch from one non-zero value to another as trajectories cross the manifold.

Theorem 2: Region of Attraction

For the system given by Equation (1) and sliding surface given by Equation (2), the subspace for which the $\{ \mathbf{x} \in \mathbb{R}^n : \sigma(\mathbf{x})=\mathbf{0} \}$ surface is reachable is given by

$\{ \mathbf{x} \in \mathbb{R}^n : \sigma^{\text{T}}(\mathbf{x})\dot{\sigma}(\mathbf{x}) < 0 \}$

That is, when initial conditions come entirely from this space, the Lyapunov function candidate $V(σ)$ is a Lyapunov function and 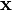$\mathbf{x}$ trajectories are sure to move toward the sliding mode surface where $\sigma( \mathbf{x} ) = \mathbf{0}$ . Moreover, if the reachability conditions from Theorem 1 are satisfied, the sliding mode will enter the region where $\dot{V}$ is more strongly bounded away from zero in finite time. Hence, the sliding mode $σ = 0$ will be attained in finite time.

Theorem 3: Sliding Motion

Let

$\frac{\partial \sigma}{\partial{\mathbf{x}}} B(\mathbf{x},t)$

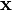be nonsingular. That is, the system has a kind of controllability that ensures that there is always a control that can move a trajectory to move closer to the sliding mode. Then, once the sliding mode where $\sigma(\mathbf{x}) = \mathbf{0}$ is achieved, the system will stay on that sliding mode. Along sliding mode trajectories, $\sigma(\mathbf{x})$ is constant, and so sliding mode trajectories are described by the differential equation

$\dot{\sigma} = \mathbf{0}$ .

If an $\mathbf{x}$ -equilibrium is stable with respect to this differential equation, then the system will slide along the sliding mode surface toward the equilibrium.

The equivalent control law on the sliding mode can be found by solving

$\dot\sigma(\mathbf{x})=0$

for the equivalent control law $\mathbf{u}(\mathbf{x})$ . That is,

$\frac{\partial \sigma}{\partial \mathbf{x}} \overbrace{\left( f(\mathbf{x},t) + B(\mathbf{x},t) \mathbf{u} \right)}^{\dot{\mathbf{x}}} = \mathbf{0}$

and so the equivalent control

$\mathbf{u} = -\left( \frac{\partial \sigma}{\partial \mathbf{x}} B(\mathbf{x},t) \right)^{-1} \frac{\partial \sigma}{\partial \mathbf{x}} f(\mathbf{x},t)$

That is, even though the actual control $\mathbf{u}$ is not continuous, the rapid switching across the sliding mode where $\sigma(\mathbf{x})=\mathbf{0}$ forces the system to act as if it were driven by this continuous control.

Likewise, the system trajectories on the sliding mode behave as if

$\dot{\mathbf{x}} = \overbrace{f(\mathbf{x},t) - B(\mathbf{x},t) \left( \frac{\partial \sigma}{\partial \mathbf{x}} B(\mathbf{x},t) \right)^{-1} \frac{\partial \sigma}{\partial \mathbf{x}} f(\mathbf{x},t)}^{f(\mathbf{x},t) + B(\mathbf{x},t) u} = f(\mathbf{x},t)\left( \mathbf{I} - B(\mathbf{x},t) \left( \frac{\partial \sigma}{\partial \mathbf{x}} B(\mathbf{x},t) \right)^{-1} \frac{\partial \sigma}{\partial \mathbf{x}} \right)$

The resulting system matches the sliding mode differential equation

$\dot{\sigma}(\mathbf{x}) = \mathbf{0}$

and so as long as the sliding mode surface where $\sigma(\mathbf{x})=\mathbf{0}$ is stable (in the sense of Lyapunov), the system can be assumed to follow the simpler $\dot{\sigma} = 0$ condition after some initial transient during the period while the system finds the sliding mode. The same motion is approximately maintained provided the equality $\sigma(\mathbf{x}) = \mathbf{0}$ only approximately holds.

It follows from these theorems that the sliding motion is invariant (i.e., insensitive) to sufficiently small disturbances entering the system through the control channel. That is, as long as the control is large enough to ensure that $\sigma^{\text{T}} \dot{\sigma} < 0$ and $\dot{\sigma}$ is uniformly bounded away from zero, the sliding mode will be maintained as if there was no disturbance. The invariance property of sliding mode control to certain disturbances and model uncertainties is its most attractive feature; it is strongly robust.

As discussed in an example below, a sliding mode control law can keep the constraint

$\dot{x} + x = 0$

in order to asymptotically stabilize any system of the form

$\ddot{x}=a(t,x,\dot{x}) + u$

when $a(\cdot)$ has a finite upper bound. In this case, the sliding mode is where

$\dot{x} = -x$

(i.e., where $\dot{x}+x=0$ ). That is, when the system is constrained this way, it behaves like a simple stable linear system, and so it has a globally exponentially stable equilibrium at the $(x,\dot{x})=(0,0)$ origin.

Control design examples

Sliding mode observer

Sliding mode control can be used in the design of state observers. These non-linear high-gain observers have the ability to bring coordinates of the estimator error dynamics to zero in finite time. Additionally, switched-mode observers have attractive measurement noise resilience that is similar to a Kalman filter. For simplicity, the example here uses a traditional sliding mode modification of a Luenberger observer for an LTI system. In these sliding mode observers, the order of the observer dynamics are reduced by one when the system enters the sliding mode. In this particular example, the estimator error for a single estimated state is brought to zero in finite time, and after that time the other estimator errors decay exponentially to zero. However, as first described by Drakunov, a sliding mode observer for non-linear systems can be built that brings the estimation error for all estimated states to zero in a finite (and arbitrarily small) time.

Here, consider the LTI system

$\begin{align} \dot{\mathbf{x}} &= A \mathbf{x} + B \mathbf{u}\\y &= \begin{bmatrix}1 & 0 & 0 & \cdots & \end{bmatrix} \mathbf{x} = x_1 \end{align}$

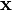where state vector $\mathbf{x} \triangleq (x_1, x_2, \dots, x_n) \in \mathbb{R}^n$ , $\mathbf{u} \triangleq (u_1, u_2, \dots, u_r) \in \mathbb{R}^r$ is a vector of inputs, and output $y$ is a scalar equal to the first state of the $\mathbf{x}$ state vector. Let

$A \triangleq \begin{bmatrix} a_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix}$

where

Hot Contents

2011/12/14

The Regular Form

Sliding mode control

Control scheme

Existence of closed-loop solutions

Theoretical foundation

Theorem 1: Existence of Sliding Mode

Reachability: Attaining sliding manifold in finite time

Theorem 2: Region of Attraction

Theorem 3: Sliding Motion

Control design examples

Sliding mode observer

See also

Notes

References

Further reading

No comments:

Post a Comment