Hot Contents: Gaussian Heath–Jarrow

Heath–Jarrow–Morton framework

The Heath–Jarrow–Morton (HJM) framework is a general framework to model the evolution of interest rate curve – instantaneous forward rate curve in particular (as opposed to simple forward rates). When the volatility and drift of the instantaneous forward rate are assumed to be deterministic, this is known as the Gaussian Heath–Jarrow–Morton (HJM) Model of forward rates . For direct modeling of simple forward rates please see the Brace–Gatarek–Musiela Model as an example.

The HJM framework originates from the work of David Heath, Robert A. Jarrow and Andrew Morton in the late 1980s, especially Bond pricing and the term structure of interest rates: a new methodology (1987) – working paper, Cornell University, and Bond pricing and the term structure of interest rates: a new methodology (1989) – working paper (revised ed.), Cornell University.

Framework

The key to these techniques is the recognition that the drifts of the no-arbitrage evolution of certain variables can be expressed as functions of their volatilities and the correlations among themselves. In other words, no drift estimation is needed.

Models developed according to the HJM framework are different from the so called short-rate models in the sense that HJM-type models capture the full dynamics of the entire forward rate curve, while the short-rate models only capture the dynamics of a point on the curve (the short rate).

However, models developed according to the general HJM framework are often non-Markovian and can even have infinite dimensions. A number of researchers have made great contributions to tackle this problem. They show that if the volatility structure of the forward rates satisfy certain conditions, then an HJM model can be expressed entirely by a finite state Markovian system, making it computationally feasible. Examples include a one-factor, two state model (O. Cheyette, "Term Structure Dynamics and Mortgage Valuation", Journal of Fixed Income, 1, 1992; P. Ritchken and L. Sankarasubramanian in "Volatility Structures of Forward Rates and the Dynamics of Term Structure", Mathematical Finance, 5, No. 1, Jan 1995), and later multi-factor versions.

Mathematical formulation

The class of models developed by Heath, Jarrow and Morton (1992) is based on modeling the forward rates, yet it does not capture all of the complexities of an evolving term structure.

The instantaneous forward rate $f \left(t,T\right),t\leq T$ is the continuous compounding rate available at time $\, T$ as seen from time $\, t$ . It is defined by:

$f\left(t,T\right)=-\frac{1}{P\left(t,T\right)}\frac{\partial}{\partial T}P\left(t,T\right)=-\frac{\partial \textrm{log} P\left(t,T\right)}{\partial T},$ (1)

The basic relation between the rates and the bond prices is given by:

$P\left(t,T\right)=e^{-\int_t^T f\left(t,s\right)\,ds}.$ (2)

Consequently, the bank account 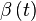$\beta\left(t\right)$ grows according to:

$\beta\left(t\right)=e^{\int_0^t f\left(s,s\right)\,ds}$ (3)

since the spot rate at time $t$ is $r(t) = f(t,t)$ .

The assumption of the HJM model is that the forward rates $f\left(t,T\right)$ satisfy for any $\, T$ :

$df\left(t,T\right)=\mu\left(t,T\right)dt+\xi\left(t,T\right)dW\left(t\right)$ (4)

where the processes $\mu\left(t,T\right),\xi\left(t,T\right)$ are continuous and adapted.

For this assumption to be compatible with the assumption of the existence of martingale measures we need the following relation to hold:

$\frac{dP\left(t,T\right)}{P\left(t,T\right)}=\left[r\left(t\right)-\alpha\left(t,T\right)\theta\left(t\right)\right]dt +\alpha\left(t,T\right)dW\left( t\right).$ (5)

We find the return on the bond in the HJM model and compare it (5) to obtain models that do not allow for arbitrage.

Let

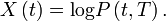$X\left(t\right)=\textrm{log} P\left(t,T\right).$ (6)

Then

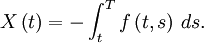$X\left(t\right)=-\int_t^T f\left(t,s\right)\,ds.$ (7)

Using Leibniz's rule for differentiating under the integral sign we have that:

$dX=-d\left(\int_t^T f\left(t,s\right) d s\right)=-A\left(t,T\right)dt-\tau\left(t,T\right)dW\left(t\right),$ (8)

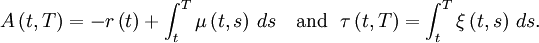
where $A\left(t,T\right)=-r\left(t\right)+\int_t^T\mu\left(t,s\right)\,ds~~~\textrm{and}~~\tau\left(t,T\right)=\int_t^T\xi\left(t,s\right)\,ds.$

By Itō's lemma,

$\frac{dP\left(t,T\right)}{P\left(t,T\right)}=dX+\frac{1}{2}(dX)^2.$ (9)

It follows from (5) and (9), we must have that

$\alpha(t,T)=-\int_t^T\xi\left(t,s\right)\,ds,$ (10)

$\alpha(t,T)\cdot\theta(t)=\int_t^T\mu(t,s)\,ds-\frac{1}{2}\left(\int_t^T\xi\left(t,s\right)\,ds\right)^2.$ (11)

Rearranging the terms we get that

$\int_t^T\mu(t,s) \,ds=\frac{1}{2}\left(\int_t^T\xi\left(t,s\right)\,ds\right)^2-\theta(t)\, \int_t^T\xi\left(t,s\right)\,ds.$ (12)

Differentiating both sides by $\, T$ , we have that

$\mu(t,T)=\xi\left(t,T\right)\left(\int_t^T\xi\left(t,s\right)\,ds-\theta(t)\right).$ (13)

Equation (13) is known as the no-arbitrage condition in the HJM model. Under the martingale probability measure $\ , \theta=0$ and the equation for the forward rates becomes: