Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle. The magnitude of the angle is the "amount of rotation" that separates the two rays, and can be measured by considering the length of circular arc swept out when one ray is rotated about the vertex to coincide with the other (see "Measuring angles", below). Where there is no possibility of confusion, the term "angle" is used interchangeably for both the geometric configuration itself and for its angular magnitude (which is simply a numerical quantity).
The word angle comes from the Latin word angulus, meaning "a corner". The word angulus is a diminutive, of which the primitive form, angus, does not occur in Latin. Cognate words are the Greek ἀγκύλος (ankylοs), meaning "crooked, curved," and the English word "ankle". Both are connected with the Proto-Indo-European root *ank-, meaning "to bend" or "bow".
Euclid defines a plane angle as the inclination to each other, in a plane, of two lines which meet each other, and do not lie straight with respect to each other. According to Proclus an angle must be either a quality or a quantity, or a relationship. The first concept was used by Eudemus, who regarded an angle as a deviation from a straight line; the second by Carpus of Antioch, who regarded it as the interval or space between the intersecting lines; Euclid adopted the third concept, although his definitions of right, acute, and obtuse angles are certainly quantitative.
Measuring angles
Two angles are sometimes called congruent if there exists an isometry that transforms one of the angles into the other angle. The size of an angle is normally characterized by the smallest positive rotation that maps one of the rays into the other. Two angles are congruent if and only if they correspond to the same (smallest positive) rotation. Thus an angle as two rays is characterized by an angle of rotation. To avoid confusion when no isometry exists between particular representations of angles, angles that Euclid called "equal" are described as "equal in measure".
In many geometrical situations, angles that differ by an exact multiple of a full circle are effectively equivalent (it makes no difference how many times a line is rotated through a full circle because it always ends up in the same place). However, this is not always the case. For example, when tracing a curve such as a spiral using polar coordinates, an extra full turn gives rise to a quite different point on the curve.
In order to measure an angle θ, a circular arc centered at the vertex of the angle is drawn, e.g. with a pair of compasses. The length of the arc s is then divided by the radius of the circle r, and possibly multiplied by a scaling constant k (which depends on the units of measurement that are chosen):
The value of θ thus defined is independent of the size of the circle: if the length of the radius is changed then the arc length changes in the same proportion, so the ratio s/r is unaltered.
Units
In dimensional analysis, angles are considered to be dimensionless. There are several units used to measure angles, depending on the choice of the constant k in the formula above. Of these units, treated in more detail below, the degree and the radian are by far the most common.
With the notable exception of the radian, most units of angular measurement are defined such that one full circle (i.e. one turn) is equal to n units, for some whole number n. For example, in the case of degrees, n = 360. A full circle of n units is obtained by setting k = n/(2π) in the formula above. (Proof. The formula above can be rewritten as k = θr/s. One full circle, for which θ = n units, corresponds to an arc equal in length to the circle's circumference, which is 2πr, so s = 2πr. Substituting n for θ and 2πr for s in the formula, results in k = nr/(2πr) = n/(2π).)
Positive and negative angles
In mathematics the angle from the first to the second coordinate axis of a coordinate system is considered as positive. Therefore angles given a sign are positive angles if measured anticlockwise, and negative angles if measured clockwise, from a given line. If no line is specified, it can be assumed to be the first coordinate axis (x-axis) in the Cartesian plane. In many geometrical situations a negative angle of −θ is effectively equivalent to a positive angle of "one full turn less θ". For example, a clockwise rotation of 45° (that is, an angle of −45°) is often effectively equivalent to an anticlockwise rotation of 360° − 45° (that is, an angle of 315°).
In three dimensional geometry, "clockwise" and "anticlockwise" have no absolute meaning, so the direction of positive and negative angles must be defined relative to some reference, which is typically a vector passing through the angle's vertex and perpendicular to the plane in which the rays of the angle lie.
In navigation, bearings are measured from north, increasing clockwise, so a bearing of 45 degrees is north-east. Negative bearings are not used in navigation, so north-west is 315 degrees.
Alternative ways of measuring the size of an angle
There are several alternatives to measuring the size of an angle by the corresponding angle of rotation. The grade of a slope, or gradient is equal to the tangent of the angle, or sometimes the sine. Gradients are often expressed as a percentage. For very small values (less than 5%), the grade of a slope is approximately the measure of an angle in radians.
In rational geometry the spread between two lines is defined at the square of sine of the angle between the lines. Since the sine of an angle and the sine of its supplementary angle are the same any angle of rotation that maps one of the lines into the other leads to the same value of the spread between the lines.
Astronomical approximations
Astronomers measure angular separation of objects in degrees from their point of observation.
These measurements clearly depend on the individual subject, and the above should be treated as rough approximations only.
Identifying angles
In mathematical expressions, it is common to use Greek letters (α, β, γ, θ, φ, ...) to serve as variables standing for the size of some angle. (To avoid confusion with its other meaning, the symbol π is typically not used for this purpose.) Lower case roman letters (a, b, c, ...) are also used. See the figures in this article for examples.
In geometric figures, angles may also be identified by the labels attached to the three points that define them. For example, the angle at vertex A enclosed by the rays AB and AC (i.e. the lines from point A to point B and point A to point C) is denoted ∠BAC or BÂC. Sometimes, where there is no risk of confusion, the angle may be referred to simply by its vertex ("angle A").
Potentially, an angle denoted, say, ∠BAC might refer to any of four angles: the clockwise angle from B to C, the anticlockwise angle from B to C, the clockwise angle from C to B, or the anticlockwise angle from C to B, where the direction in which the angle is measured determines its sign (see Positive and negative angles). However, in many geometrical situations it is obvious from context that the positive angle less than or equal to 180 degrees is meant, and no ambiguity arises. Otherwise, a convention may be adopted so that ∠BAC always refers to the anticlockwise (positive) angle from B to C, and ∠CAB to the anticlockwise (positive) angle from C to B.
Types of angles
A formal definition
Using trigonometric functions
A Euclidean angle is completely determined by the corresponding right triangle. In particular, if θ is a Euclidean angle, it is true that
and
for two numbers x and y. So an angle in the Euclidean plane can be legitimately given by two numbers x and y.
To the ratio y/x there correspond two angles in the geometric range 0 < θ < 2π, since
Angles between curves
The angle between a line and a curve (mixed angle) or between two intersecting curves (curvilinear angle) is defined to be the angle between the tangents at the point of intersection. Various names (now rarely, if ever, used) have been given to particular cases:—amphicyrtic (Gr. ἀμφί, on both sides, κυρτός, convex) or cissoidal (Gr. κισσός, ivy), biconvex; xystroidal or sistroidal (Gr. ξυστρίς, a tool for scraping), concavo-convex; amphicoelic (Gr. κοίλη, a hollow) or angulus lunularis, biconcave.
Dot product and generalisation
In the Euclidean plane, the angle θ between two vectors u and v is related to their dot product and their lengths by the formula
This formula supplies an easy method to find the angle between two planes (or curved surfaces) from their normal vectors and between skew lines from their vector equations.
Inner product
To define angles in an abstract real inner product space, we replace the Euclidean dot product ( · ) by the inner product 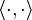 , i.e.
, i.e.
In a complex inner product space, the expression for the cosine above may give non-real values, so it is replaced with
or, more commonly, using the absolute value, with
The latter definition ignores the direction of the vectors and thus describes the angle between one-dimensional subspaces 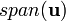 and
and  spanned by the vectors
spanned by the vectors 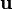 and
and  correspondingly.
correspondingly.
Angles between subspaces
The definition of the angle between one-dimensional subspaces 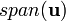 and
and  given by
given by
in a Hilbert space can be extended to subspaces of any finite dimensions. Given two subspaces  with
with 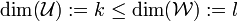 , this leads to a definition of k angles called canonical or principal angles between subspaces.
, this leads to a definition of k angles called canonical or principal angles between subspaces.
Angles in Riemannian geometry
In Riemannian geometry, the metric tensor is used to define the angle between two tangents. Where U and V are tangent vectors and gij are the components of the metric tensor G,
Angles in geography and astronomy
In geography, the location of any point on the Earth can be identified using a geographic coordinate system. This system specifies the latitude and longitude of any location in terms of angles subtended at the centre of the Earth, using the equator and (usually) the Greenwich meridian as references.
In astronomy, a given point on the celestial sphere (that is, the apparent position of an astronomical object) can be identified using any of several astronomical coordinate systems, where the references vary according to the particular system. Astronomers measure the angular separation of two stars by imagining two lines through the centre of the Earth, each intersecting one of the stars. The angle between those lines can be measured, and is the angular separation between the two stars.
Astronomers also measure the apparent size of objects as an angular diameter. For example, the full moon has an angular diameter of approximately 0.5°, when viewed from Earth. One could say, "The Moon subtends an angle of half a degree." The small-angle formula can be used to convert such an angular measurement into a distance/size ratio.
See also
References
![]() Chisholm, Hugh, ed (1911). "Angle". Encyclopædia Britannica (Eleventh ed.). Cambridge University Press.
Chisholm, Hugh, ed (1911). "Angle". Encyclopædia Britannica (Eleventh ed.). Cambridge University Press.
- Euclid, commentary and trans. by T. L. Heath Elements Vol. 1 (1908 Cambridge) Google Books
External links
- Angle Bisectors in a Quadrilateral at cut-the-knot
- Constructing a triangle from its angle bisectors at cut-the-knot
- Angle Estimation – for basic astronomy.
- Angle definition pages with interactive applets.
- Various angle constructions with compass and straightedge
- GonioLab DD – Convert between DecDeg and DegMinSec and vice-versa (requires Java Web Start)
Retrieved from : http://en.wikipedia.org/wiki/Angle#Types_of_angles

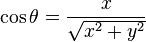
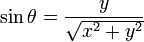

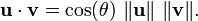
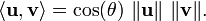



No comments:
Post a Comment